Nonlinear Estimation Framework
Description
NEF is newly designed framework for nonlinear state estimation of discrete dynamical systems. The aim of this framework is to facilitate implementation, testing and use of various nonlinear state estimation methods. The main strength of the framework is its versatility due to the possibility of either structural or probabilistic description of the problem. As the toolbox is designed on the object oriented basis, further adding of user-specified nonlinear estimation algorithms is extremely easy.
This new toolbox should overcome following deficiencies of the framework which constitues base of the NFTools:
- It should made it possible to describe system not only by difference equations. The description by probability density functions is also supported.
- It should support the specification of time-varying systems.
The key element of the new design is the unified description of random variables. It also uses the new MATLAB® class system.
The toolbox currently implements following estimators:
| Estimator | Toolbox object | Num. stable version |
|---|---|---|
| (extended) Kalman filter | nefKalman | nefUDKalman, nefSKalman |
| Unscented Kalman filter | nefUKF | nefSUKF |
| Divided difference filter 1st order | nefDD1 | nefSDD1 |
| Central difference filter | nefDD1 | nefSDD1 |
| Divided difference filter 2nd order | nefDD2 | nefSDD2 |
| Iteration filter | nefItFilter | depends on used local filter |
| Stochastic Integration Filter | nefSIF |
| Estimator | Toolbox object | Note |
|---|---|---|
| Ensemble Kalman filter | nefEnKF | |
| Gaussian sum filter | nefGSM | can utilize all of the local filters |
| Particle filter | nefPF | sampling densities: prior, optimal, EKF, auxiliary (point and functional) |
| Indetificator | Toolbox object | Note |
|---|---|---|
| autocovariance least-squares method | nefALS | for identification of noise covariance matrices |
| measurement difference autocovariance method | mefMDA | for identification of noise covariance matrices |
Requirements
This toolbox is designed for use with MATLAB® environment. Due to the use of new class systems and some other MATLAB features it requires at least version 2009b.
Publication related to the NEF
A brief introduction to the NEF framework can be found in the following articles
- O. Straka, et al. (2009). 'A software framework and tool for nonlinear state estimation' In Proceedings of the 15th IFAC Symposium on System Identification, SYSID 2009, Saint-Malo, France (poster)
- O. Straka, et al. (2010). 'Nonlinear estimation framework in target tracking' In Proceedings of the 13th International Conference on Information Fusion, Edinburgh,UK, ISBN 978-0-9824438-1-1
- M. Flídr, et. al. (2013). 'Nonlinear Estimation Framework: a Versatile Tool for State Estimation' In Proceedings of the 18th International Conference on Methods and Models in Automation and Robotics, Międzyzdroje, Poland, (conference presentation)
- M. Flídr, et al. (2014). ' Nonlinear Estimation Software Framework in Optimal and Adaptive Control Problems'. In Proceedings of the 19th IFAC World Congress, 2014. pp. 5485-5490. ISBN: 978-3-902823-62-5 , ISSN: 1474-6670, (conference presentation)
Example of experiment design
In this example, a slight modification of the tracking problem presented in
N. Gordon, D. Salmond, and A.F.M. Smith. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE proceedings-F, 140:107–113, 1993.
is considered. A ship is moving in x-y plane with the stationary observer at the origin of the plane, The ship is assumed to accelerate and decelerate randomly over time.
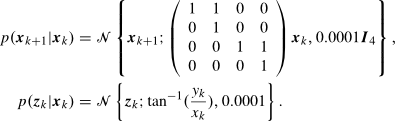
The following picture shows all the classes necessary to describe the describe the system in the estimation experiment:
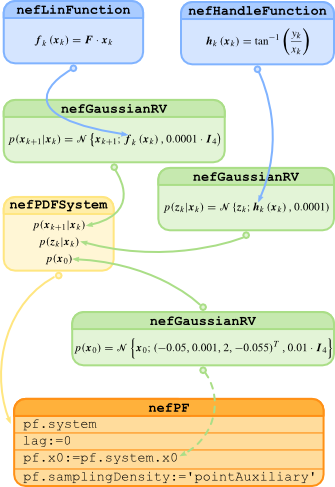
For specification of the system, the nefPDFSystem class will be used. First, the transition pdf is set using its mean and covariance matrix as F = [1 1 0 0;0 1 0 0 ;0 0 1 1 ;0 0 0 1]; Then, the measurement pdf is also given by its mean and variance as
xMean = nefLinFunction(F,[],[]);
xVariance = 0.0001*eye(4);
px = nefGaussianRV(xMean,xVariance);
mFun = @(x,u,v,t) atan(x(3)/x(1)); Now, the initial condition is specified as
zMean = nefHandleFunction(mFun,[4 0 0 0]);
zVariance = 0.0001;
pz = nefGaussianRV(zMean,zVariance);
px0 = nefGaussianRV([-0.05 0.001 2 -0.055]',0.01*eye(4)); Consequently, the system is created using probabilistic description as model = nefPDFSystem(px,pz,px0); and simulated using commands nSteps=20; where the measurement values is stored in z and values of the state x. Finally, to estimate the state using the measurement, the auxiliary particle filter will be used. It will be built by a single command specifying system description, lag 0 and type of the sampling density:
[z,x] = simulate(model,nSteps,[]); pfEstimator = nefPF(model,'samplingDensity','pointAuxiliary'); Note that no other design parameters concerning the particle filter were specified and thus the default values were used, such as default sample size is 100 samples, systematic resampling executed at each time instant.
The actual estimation is run as [estimates] = estimate(pfEstimator,z,[]); As a result, the filtering pdf estimates given by empirical pdf nefEmpiricalRV are stored in estimates.
Licence
- The NEF is copyrighted freeware provided by the Identification and Decision Making Research Group at the Departement of Cybernetics, University of West Bohemia.
- ANY TYPE OF REDISTRIBUTION AND/OR MODIFICATION OF THE TOOLBOX IS NOT PERMITTED!
- It is not permitted to use this software or any of its part for commercial purposes or include it or its part in commercial products without prior written consent of copyright holders represented by current maintainer of the NEF.
- In case of publication of results obtained using the software you are bound to either name the NEF with the web page of the toolbox and our institution (i.e.Departement of Cybernetics, University of West Bohemia) or cite at least one reference to recent publication on the NEF (to be found at http://nft.kky.zcu.cz/)
- THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
- MATLAB is trademark of The MathWorks, Inc.
Download
To download this tool, go to download page.