Toolbox for State Estimation of Nonlinear Discrete Time Stochastic Systems
Description
NFTools is a toolbox for state estimation of discrete time nonlinear stochastic systems. It has been designed to provide means for all necessary steps for proceeding with state estimation experiment. It allows system design, system simulation, estimator setup and state estimation. The toolbox can be easily extended with user defined estimators and thus it is suitable for estimator testing and quality comparison of different estimators. The list of currently implemented estimators is shown in the following table:
| Estimator | Toolbox object |
|---|---|
| Kalman filter | kalman |
| Extended Kalman filter | extkalman |
| Iterated Kalman filter | itekalman |
| Second order filter | seckalman |
| Unscented Kalman filter | ukf |
| Divided difference filters | dd1, dd2 |
| Central Difference Filter | dd1 |
| Gaussian sum method | gsm |
| Point Mass Method | pmf |
Requirements
This toolbox is designed for use with MATLAB® environment (version 6.x and 7.x). The second (optional, however recomended) requirement is the Symbolic Math Toolbox.
Publication related to the NFTools
A more detailed description of the NFTools and brief introduction to the state estimation is given in:
- M. Šimandl, et al. (2003). 'Nonlinear Filtering Toolbox'. Technical Report, Department of Cybernetics, University Of West Bohemia. (English language).
- M. Šimandl, et al. (2004). 'Nonlinear filtering methods: basic approaches and software package'. In Preprints of the CMP'04, Prague. (English language).
- R. Sedlák (2004). 'Referenční příručka'. Technical Report, Department of Cybernetics, University Of West Bohemia. (Czech language).
- M. Flídr, et al. (2006). 'Framework for implementing and testing nonlinear filters', In Preprints of the 7th IFAC Symposium on Advances in Control Education, Madrid, Spain.
Example of experiment design
The capabilities of the NFTools will be presented on a simple example. Consider the following discrete stochastic system
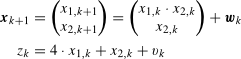
where the stochastic quantities wk and vk are described by the following probability density functions
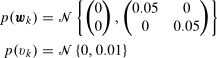
and the probability density function of the initial state x0 is ![]()
The design of estimation experiment proceeds mostly through the following steps:
- description of the probability density function of state and measurement noise and of the prior state
- description of the state update and measurement relations
- definition of the system
- simulation of system
- specification of the estimator
- estimation of the state
In the first step it is thus neccessary to create object describing the probability density function. In this case all the densities are Gaussian and instances of class gpdf will created issuing the commands pv = gpdf(0,0.01);
pw = gpdf([0;0],0.05*eye(2));
px0 = gpdf([0.9;-0.85],diag([0.09,10^-1]));
Now it is necessary to define the state update and measuremrnt relations. The state update difference relation is nonlinear an for its description the class gnfSymFunction will be used f = nfSymFunction('[x1^2*x2+w1;x2+w2]','','x1,x2','w1,w2'); The measurement is a linear function described within toolbox by object created in the following manner H = [4 1];
Delta = 1;
h = nfLinFunction(H,[],Delta,'','x1,x2','v')
Having created objects representing the random quantities and the function describing the system , it is now possible to create an entire model issuing the following constructor of the nlga class referring to NonLinear system with Gaussian Additive noises system = nlga(f,h,pw,pv,px0) The object system represents an instance of the nlga class.
The trajectory of the system can be simulated using the simulate method for n time instants issuing the following commands n = 40; where the method parameter u represents know input of the system.
u = zeros(1,n);
[measurement,stateTrajectory,system] = simulate(system,u,n);
In the next step it is time to create object that describes the estimator. In this special case let's consider that the prior probability density function of the initial estimate is different from the state prior probability density function
![]()
represented by the object px0_est = gpdf([9;-0.85],eye(2)); Now the the object that implements the square-root version of the unscented kalman filer for the case of one step smoothing is created using command lag = -1;
filterSUKF = ukf(system,lag,px0_est,'squareroot');
The final step is to execute command that processes the data and computes the estimates of the state. This is acomplished by the command [stateEstimates,filterSUKF] = estimate(filterSUKF,measurement,[]);
Licence
- The NFTools is copyrighted freeware provided by the Identification and Decision Making Research Group at the Departement of Cybernetics, University of West Bohemia.
- ANY TYPE OF REDISTRIBUTION AND/OR MODIFICATION OF THE TOOLBOX IS NOT PERMITTED!
- It is not permitted to use this software or any of its part for commercial purposes or include it or its part in commercial products without prior written consent of copyright holders represented by current maintainer of the NFTools.
- In case of publication of results obtained using the software you are bound to either name the NFTools with the web page of the toolbox and our institution (i.e.Departement of Cybernetics, University of West Bohemia) or cite at least one reference to recent publication on the NFTools (to be found at http://nft.kky.zcu.cz/)
- THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
- MATLAB and the Symbolic Math Toolbox are trademarks of The MathWorks, Inc.
Download
To download this tool, go to download page.