Nonlinear Filtering Toolbox for Continuous stochastic systems with Discrete measurements
Description
NFTCD is toolbox designed for state estimation of continuous stochastic systems with discrete-time measurements. It serves for system design, system simulation, estimator setup and state estimation. The toolbox can be easily extended with user defined estimators and thus it is suitable for estimator testing and quality comparison of different estimators. The list of currently implemented estimators is shown in the following table:
| Estimator | Toolbox object |
|---|---|
| Kalman-Bucy filter | kalmancd |
| Extended Kalman-Bucy filter | extkalmancd |
| Iterated Kalman-Bucy filter | itekalmancd |
| Second order Kalman-Bucy filter | seckalmancd |
| Gaussian sum filter | gsmcd |
| Numerical filter | nmcd |
| Particle filter | pfcd |
Requirements
This toolbox is designed for use with MATLAB® environment (version 6.x and 7.x). The second neccesary requirement is the Symbolic Math Toolbox.
Publication related to the NFTCD
An introductory description of the toolbox can be found in the following paper:
- J. Švácha, et al. (2006). 'Nonlinear Filtering Toolbox for Continuous stochastic systems with Discrete measurements', In Preprints of the 7th IFAC Symposium on Advances in Control Education, Madrid, Spain.
Example of experiment design
The capabilities of the NFTCD will be illustrated on a simple example. This example gives a short insight on how the user can exploit the features provided by the toolbox. Further, it is shown that the NFTCD represents an easy tool even for solving complex tasks.
Consider the following continuous stochastic process x(t) observed at discrete time instants t0 = 0s, t1 = 0.1s, t2 = 0.2 s, …
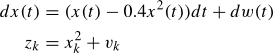
with given prior pdf
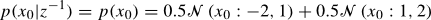
The the state and measurement noises are considered with normalized normal probability density functions.
The Gaussian sum method and the extended Kalman-Bucy filter (EKBF) were chosen for state estimation of this simple system. The prior probability density function of the initial state for the EKBF is derived from equality of the mean and the variance as
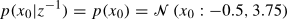
Firstly, it is necessary to create the objects representing the probability density functions of the initial condition of the state and the measurement noise. For this purpose the classes gpdf and gspdf describing the Gaussinan probability density function and Gaussian mixture, respectivelly are used in the following manner alpha0 = [0.5; 0.5];
x0 = {[-2]; [1]};
P0 = {[1]; [2]};
px0 = gspdf(alpha0,x0,P0);
px0_ekbf = gpdf(-0.5,3.75);
pw = gpdf(0,1);
pv = gpdf(0,1);
Now it is possible to create objects representing the Itô stochatic differential equation describing the dynamics of the continuous system sys_sde = sdeito('x-0.4*x^2','1','x','w',pw, px0); and the measurement equation sys_oe = oe('x^2','x','v',pv); Having these two objects an instance of a class nlngacd representing the whole system can be created system = nlngacd(sys_sde,sys_oe);
The simulation of the system trajectory is accomplished using the simulate method of the nlngacd class by employing the Euler scheme type on time interval T with the sample period Delta in the following way scheme.type = 'euler'; where time variable represents the measurement times.
scheme.T = 2;
scheme.Delta = 0.001;
time = [0:0.1:scheme.T];
[system,state,stateDelta,measurement,winc,v] = simulate(system, scheme, time);
Now it is possible to prepare the objects representing the chosen estimator. For this purpos the classes gsmcd and extkalmancd refering to Gaussian sum filter and extented Kalman-Bucy filter, respectivelly, offered by the NFTCD toolbox will be used filter_gsm = gsmcd(system,time,0); where the value 0 represents filtering problem (other variants with the parameters not equal to zero (i.e. for smoothing or prediction) are not implemented in the current version NFTCD.
filter_ekbf = extkalmancd(system,time,0);
The estimation experiment for the Gaussian sum filter is executed issuing the following commands scheme.type = 'euler'; where structure scheme specifies the Euler numerical method for solving the deterministic differential equation and the input parameter pred_num gives the number of predictive estimates in the prediction step. The output parameters estimates_gsm, predall_gsm and pred_gsm contain an array of conditional filtering probability density functions of the state xk, and conditional predictive probability density functions of state x(t) and xk, respectively. All the probability density functions are represented as instances of the gspdf class.
scheme.N = 10;
[estimates_gsm,predall_gsm,pred_gsm] = extestimate(filter_gsm,measurement,pred_num,scheme);
The estimation using the extended Kalman-Bucy filter is executed analogously [est_ekbf,predall_ekbf,pred_ekbf] = extestimate(filter_ekbf,measurement,pred_num,scheme);
The following picture compares the results of the estimation experiments.
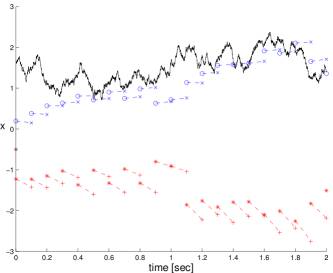
where the state x(t) is represented by solid line, the estimates delivered by the Gaussina sum filter are blue and the estimates delivered by the extended Kalman-Bucy filter are red. (Note that the EKBF generates state estimates which diverge from the state. This fact is caused by the quadratic measurement function.)
Licence
- The Nonlinear Filtering Toolbox for Continuous stochastic systems with Discrete measurements is copyrighted freeware provided by the Identification and Decision Making Research Group at the Departement of Cybernetics, University of West Bohemia.
- ANY TYPE OF REDISTRIBUTION AND/OR MODIFICATION OF THE TOOLBOX IS NOT PERMITTED!
- It is not permitted to use this software or any of its part for commercial purposes or include it or its part in commercial products without prior written consent of copyright holders represented by current maintainer of the Nonlinear Filtering Toolbox for Continuous stochastic systems with Discrete measurements.
- In case of publication of results obtained using the software you are bound to either name the Nonlinear Filtering Toolbox for Continuous stochastic systems with Discrete measurements with the web page of the toolbox and our institution (i.e.Departement of Cybernetics, University of West Bohemia) or cite at least one reference to recent publication on the Nonlinear Filtering Toolbox for Continuous stochastic systems with Discrete measurements (to be found at http://nft.kky.zcu.cz/)
- THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
- MATLAB and the Symbolic Math Toolbox are trademarks of The MathWorks, Inc.
Download
To download this tool, go to download page.